2-3-4 Tree也叫2-4 Tree
其实是B tree的一个特例,也就是个多路搜索树
CRUD
R read
find 47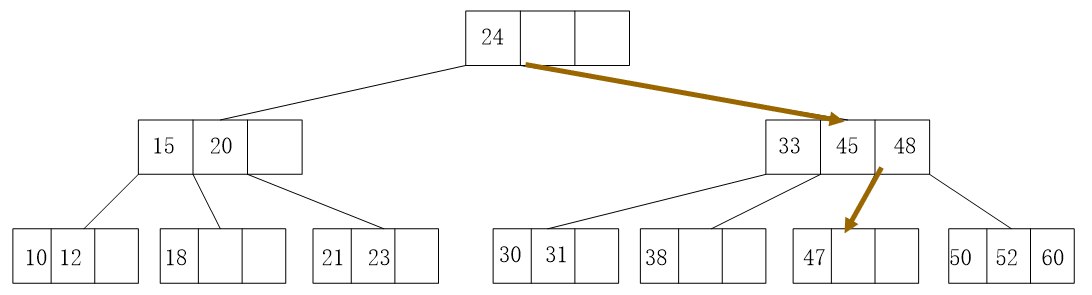
C insert
insert 30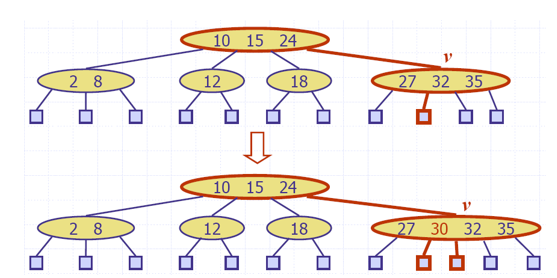
overflow: split,32提上去,两个兄弟分家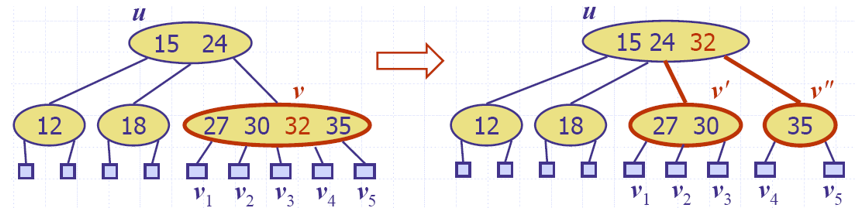
D delete
delete 24,27提上去补位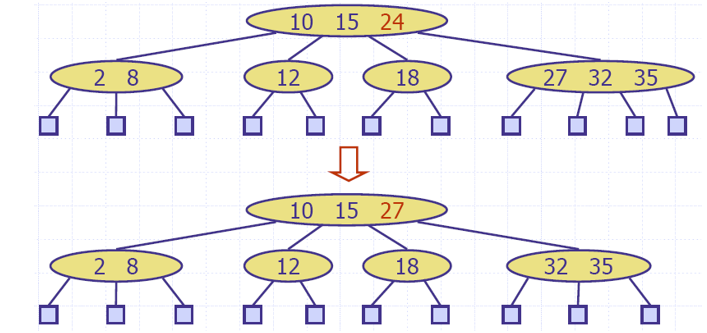
Red Black Tree
就是2-4 Tree的Binary Search Tree(BST)表达方法,中间的key提上来做黑色parent,同一个node的其他两个key做红孩子,就变成BST了
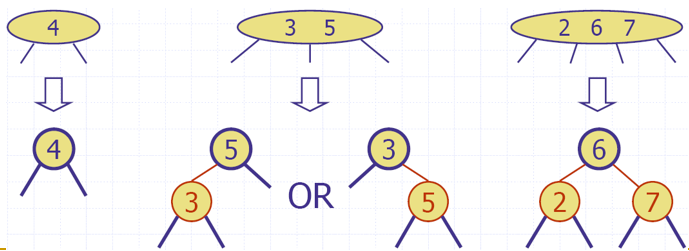
性质4条,前3条就是24树自然推导的,最后一条man made
- 所以根肯定黑的
- 所有叶子的黑色深度是一样的,因为24树本来就平衡的
- 红node的孩子是黑的,其实就是偏门key的孩子
- 叶子是黑的:强行加个null叶子
CRUD
动画:https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
怎么rotate见Splay和AVL Tree
C
- 正常BST插入,涂成红色(也就是默认是偏门的key)
- 递归解决双红冲突:
- parent是个黑的:搞定,(对应没有overflow,直接插个偏门key)
- parent是个红的:
- 叔叔是个黑的:RR LL LR RL rotation
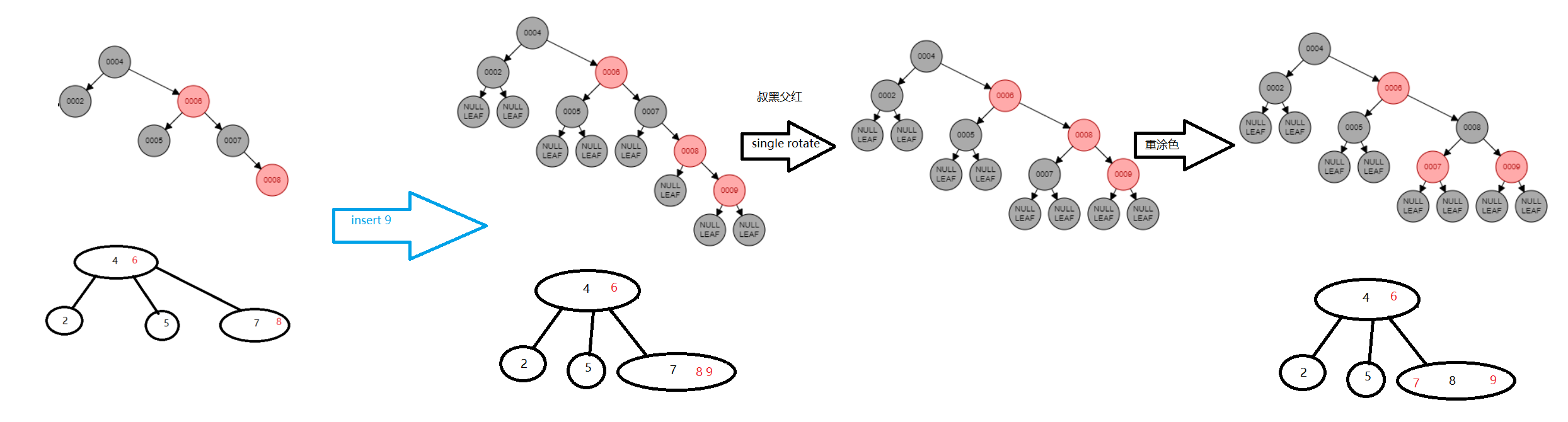
- 叔叔是个红的:直接把上一代人涂黑,两个兄弟自立门户,祖父涂成红色,提上去做上一代的偏门key,(对应overflow,split)
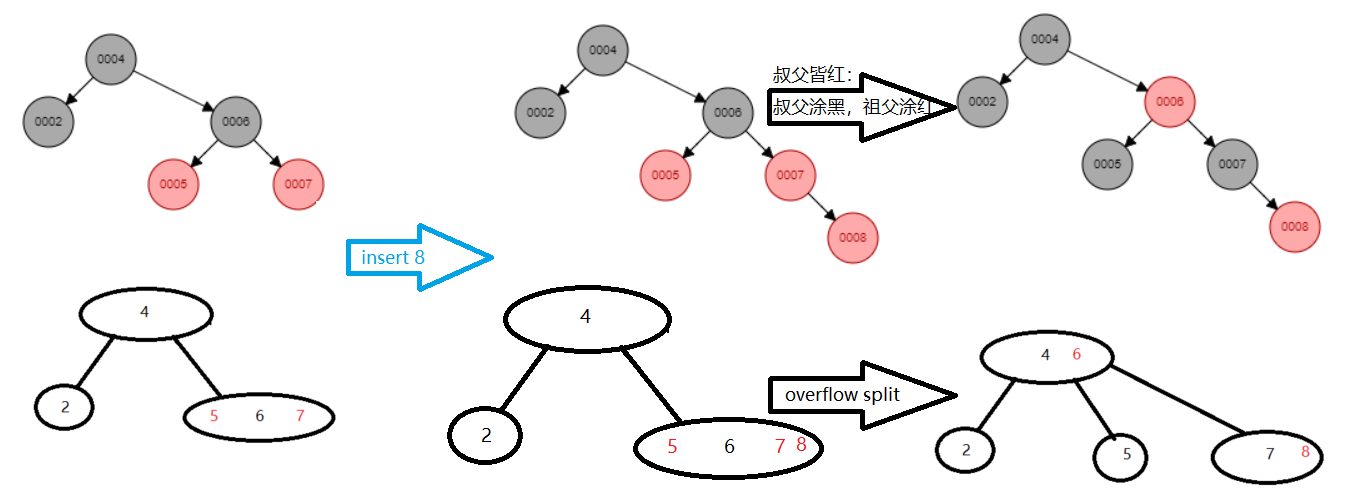
- 叔叔是个黑的:RR LL LR RL rotation
D
- 正常BST删除
- 递归解决冲突
- 原来(被删的)是个红的,或者,替上来的是个红的,涂成黑色搞定,对应把偏门key提上来做中间key
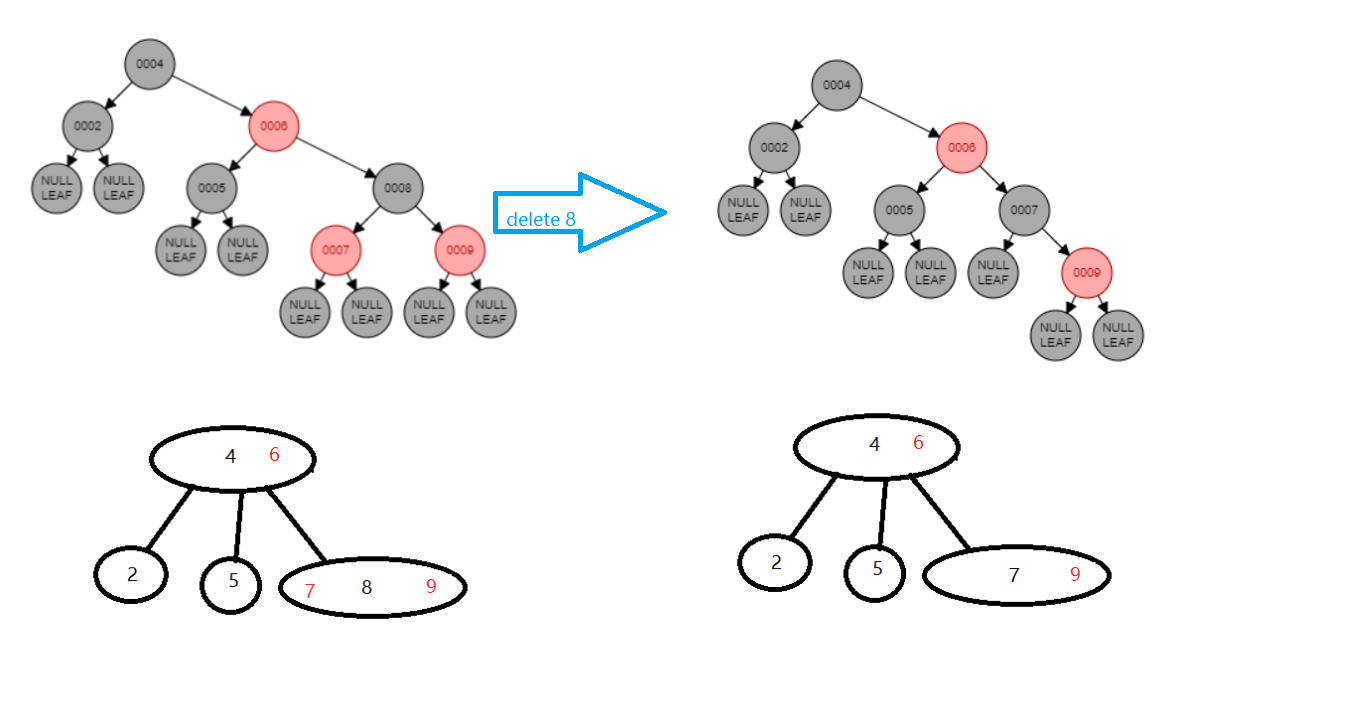
- 原来和替上来的全是黑的(双黑)
- 兄弟是黑的,有至少一个个红侄子:rotate
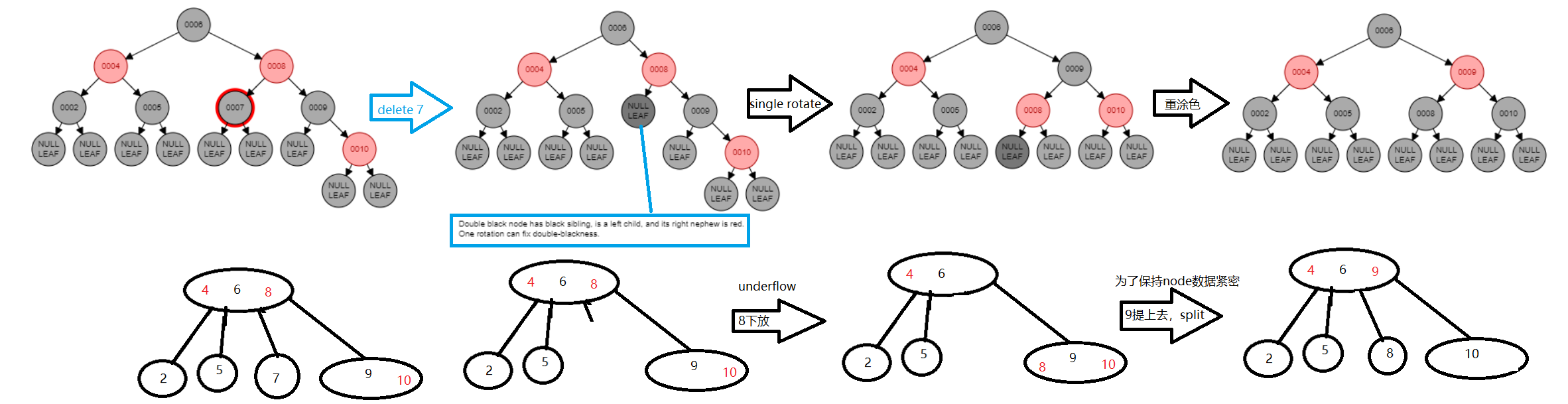
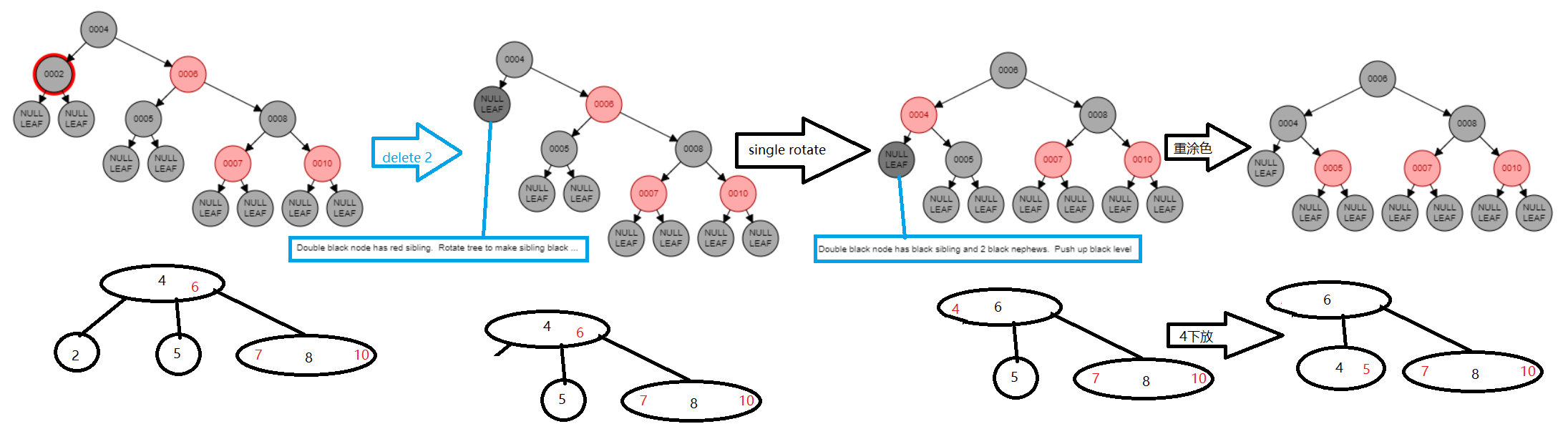
- 兄弟是黑的,有一双黑侄子:重新上色:兄弟变成红的,parent变成黑的,自立门户,吸收兄弟做偏门key
- 兄弟是红的:single rotation,重新涂色
- 兄弟是黑的,有至少一个个红侄子:rotate
- 原来(被删的)是个红的,或者,替上来的是个红的,涂成黑色搞定,对应把偏门key提上来做中间key